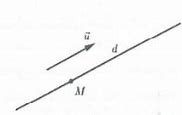
Vectơ Chỉ Phương Trong Không Gian Oxyz

Như vậy, điều kiện để 3 vectơ đồng phẳng trong không gian Oxyz là gì? Cách để chứng minh ba vectơ đồng phẳng như thế nào? chúng ta cùng tìm hiểu qua bài viết dưới đây.

Bài tập trắc nghiệm về góc trong không gian có đáp án chi tiết

Bài tập 1: Cho hai mặt phẳng $(P):2x-y-2z-5=0$ và $(Q):x-y+1=0$. Góc giữa hai mặt phẳng (P) và (Q) là:

A. ${{30}^{o}}.$ B. ${{45}^{o}}.$ C. ${{60}^{o}}.$ D. ${{135}^{o}}.$

Ta có: $\overrightarrow{{{n}_{(P)}}}=\overrightarrow{{{n}_{1}}}=(2;-1;-2);\overrightarrow{{{n}_{(Q)}}}=\overrightarrow{{{n}_{2}}}=(1;-1;0)$

Khi đó: $\cos \left( (P);(Q) \right)=\left| \cos \left( \overrightarrow{{{n}_{1}}};\overrightarrow{{{n}_{2}}} \right) \right|=\frac{\left| 2.1+2-2.0 \right|}{\sqrt{4+1+4}.\sqrt{2}}=\frac{3}{3\sqrt{2}}=\frac{1}{\sqrt{2}}\Rightarrow \widehat{\left( (P);(Q) \right)}={{45}^{0}}$

Bài tập 2: Cho hai mặt phẳng $(P):2x-y+2z-1=0$ và $(Q):x+2y-z+3=0$. Gọi $\alpha $ là góc giữa hai mặt phẳng (P) và (Q) khi đó $\cos \alpha $ bằng

A. $-\frac{\sqrt{6}}{9}.$ B. $\frac{-2\sqrt{5}}{15}.$ C. $\frac{2\sqrt{5}}{15}.$ D. $\frac{\sqrt{6}}{9}.$

Ta có $\overrightarrow{{{n}_{(P)}}}=\overrightarrow{{{n}_{1}}}=(2;-1;2);\overrightarrow{{{n}_{(Q)}}}=\overrightarrow{{{n}_{2}}}=(1;2;-1)$

Khi đó: $\cos \alpha =\left| \cos \left( \overrightarrow{{{n}_{1}}};\overrightarrow{{{n}_{2}}} \right) \right|=\frac{\left| 2-2-2 \right|}{\sqrt{4+1+4}.\sqrt{1+4+1}}=\frac{2}{3\sqrt{6}}=\frac{\sqrt{6}}{9}.$

Bài tập 3: Cho hai mặt phẳng $(P):mx+2y+mz-12=0$ và $(Q):x+my+z+3=0$. Có bao nhiêu giá trị của m sao cho góc giữa hai mặt phẳng $(P)$ và (Q) bằng ${{45}^{o}}$

Ta có: $\overrightarrow{{{n}_{(P)}}}=\overrightarrow{{{n}_{1}}}=(m;2;m);\overrightarrow{{{n}_{(Q)}}}=\overrightarrow{{{n}_{2}}}=(1;m;1)$

Khi đó: $\cos {{45}^{o}}=\left| \cos \left( \overrightarrow{{{n}_{1}}};\overrightarrow{{{n}_{2}}} \right) \right|=\frac{\left| m+2m+m \right|}{\sqrt{2{{m}^{2}}+4}.\sqrt{{{m}^{2}}+2}}=\frac{4\left| m \right|}{\sqrt{2}\left( {{m}^{2}}+2 \right)}$

$\Leftrightarrow \frac{\sqrt{2}}{2}=\frac{4\left| m \right|}{\sqrt{2}({{m}^{2}}+2)}\Leftrightarrow {{m}^{2}}+2=4\left| m \right|\xrightarrow{t=\left| m \right|>0}{{t}^{2}}-4t+2=0\Rightarrow t=2\pm \sqrt{2}\Rightarrow m=\pm \sqrt{2\pm \sqrt{2}}$

Bài tập 4: Cho hai mặt phẳng $(P):4x+my+mz+1=0$ và $(Q):x-y-3=0$. Có bao nhiêu giá trị của m sao cho góc giữa hai mặt phẳng $(P)$ và (Q) bằng ${{60}^{o}}$

Ta có $\overrightarrow{{{n}_{(P)}}}=\overrightarrow{{{n}_{1}}}=(4;m;m);\overrightarrow{{{n}_{(Q)}}}=\overrightarrow{{{n}_{2}}}=(1;-1;0)$

Khi đó: $\cos {{60}^{o}}=\left| \cos \left( \overrightarrow{{{n}_{1}}};\overrightarrow{{{n}_{2}}} \right) \right|=\frac{\left| 4-m \right|}{\sqrt{2{{m}^{2}}+16}.\sqrt{2}}=\frac{\left| 4-m \right|}{2\sqrt{{{m}^{2}}+8}}$

$\Leftrightarrow \frac{1}{2}=\frac{\left| 4-m \right|}{2\sqrt{{{m}^{2}}+8}}\Leftrightarrow {{m}^{2}}+8={{(4-m)}^{2}}\Leftrightarrow 8=16-8m\Leftrightarrow m=1$

Bài tập 5: Cho 2 đường thẳng ${{d}_{1}}:\frac{x}{-1}=\frac{y+1}{4}=\frac{z}{3}$ và ${{d}_{2}}:\frac{x}{1}=\frac{y+1}{-4}=\frac{z+2}{-3}$. Góc giữa ${{d}_{1}}$ và ${{d}_{2}}$ là:

A. ${{0}^{o}}.$ B. ${{30}^{o}}.$ C. ${{60}^{o}}.$ D. ${{90}^{o}}.$

$\overrightarrow{{{u}_{1}}}=(-1;4;3);\overrightarrow{{{u}_{2}}}=(1;-4;-3)\Rightarrow \cos ({{d}_{1}};{{d}_{2}})=\left| \cos \left( \overrightarrow{{{u}_{1}}};\overrightarrow{{{u}_{2}}} \right) \right|=\frac{\left| -26 \right|}{\sqrt{1+16+9}.\sqrt{1+16+9}}=1.$

Do đó $\widehat{\left( {{d}_{1}};{{d}_{2}} \right)}={{0}^{o}}.$

Bài tập 6: Cho 2 đường thẳng ${{d}_{1}}:\left\{ \begin{align} & x=t \\ & y=5-2t \\ & z=14-3t \\ \end{align} \right.$ và ${{d}_{2}}:\left\{ \begin{align} & x=1-4t \\ & y=2+t \\ & z=-1+5t \\ \end{align} \right.$. Góc giữa ${{d}_{1}}$ và ${{d}_{2}}$ là:

A. ${{0}^{o}}.$ B. ${{30}^{o}}.$ C. ${{60}^{o}}.$ D. ${{90}^{o}}.$

$\overrightarrow{{{u}_{1}}}=(1;-2;3);\overrightarrow{{{u}_{2}}}=(-4;1;5)\Rightarrow \cos ({{d}_{1}};{{d}_{2}})=\left| \cos \left( \overrightarrow{{{u}_{1}}};\overrightarrow{{{u}_{2}}} \right) \right|=\frac{\left| -4-2-15 \right|}{\sqrt{1+4+9}.\sqrt{16+1+25}}=\frac{21}{14\sqrt{3}}=\frac{\sqrt{3}}{2}.$

Suy ra $\widehat{\left( {{d}_{1}};{{d}_{2}} \right)}={{30}^{o}}.$

Bài tập 7: Cho 4 điểm $A(1;0;0);\,B(0;1;0);\,C(0;0;1)$ và $D(-2;1;-1)$. Góc giữa 2 đường thẳng AB và CD là:

A. ${{45}^{o}}.$ B. ${{30}^{o}}.$ C. ${{60}^{o}}.$ D. ${{90}^{o}}.$

Ta có: $\overrightarrow{{{u}_{AB}}}=\overrightarrow{{{u}_{1}}}=(-1;1;0);\overrightarrow{{{u}_{CD}}}=\overrightarrow{{{u}_{2}}}=(-2;1;-2)$

Khi đó: $\cos \left( \widehat{AB;CD} \right)=\left| \cos \left( \overrightarrow{{{u}_{1}}};\overrightarrow{{{u}_{2}}} \right) \right|=\frac{\left| 2+1 \right|}{\sqrt{2}.3}=\frac{1}{\sqrt{2}}\Rightarrow \left( \widehat{AB;CD} \right)={{45}^{o}}.$

Bài tập 8: Cho 2 đường thẳng ${{d}_{1}}:\frac{x-1}{2}=\frac{y}{2}=\frac{z+1}{-1}$ và ${{d}_{2}}:\frac{x+1}{1}=\frac{y-2}{-2}=\frac{z+3}{1}$. Cosin góc giữa ${{d}_{1}}$ và ${{d}_{2}}$ là:

A. $\frac{\sqrt{6}}{3}.$ B. $\frac{\sqrt{3}}{2}.$ C. $\frac{1}{\sqrt{6}}.$ D.$\frac{1}{\sqrt{2}}.$

Ta có: $\overrightarrow{{{u}_{1}}}=(2;2;-1);\overrightarrow{{{u}_{2}}}=(1;-2;1)\Rightarrow cos\left( {{d}_{1}};{{d}_{2}} \right)=\left| \cos \left( \overrightarrow{{{u}_{1}}};\overrightarrow{{{u}_{2}}} \right) \right|=\frac{\left| 2-4-1 \right|}{3.\sqrt{6}}=\frac{3}{3\sqrt{6}}=\frac{1}{\sqrt{6}}.$

Suy ra $\left( \widehat{{{d}_{1}};{{d}_{2}}} \right)={{30}^{o}}.$

Bài tập 9: Cho hai đường thẳng ${{d}_{1}}:\left\{ \begin{align} & x=-1+t \\ & y=-t\sqrt{2} \\ & z=2+t \\ \end{align} \right.$ và ${{d}_{2}}:\left\{ \begin{align} & x=2+t \\ & y=1+t\sqrt{2} \\ & z=2+mt \\ \end{align} \right.$. Tìm giá trị của m sao cho góc giữa ai đường thẳng ${{d}_{1}}$ và ${{d}_{2}}$ bằng ${{60}^{o}}.$

A. $m=1.$ B. $m=-1.$ C.$m=1$ và $m=-1.$ D.$m=0.$

Ta có: $\overrightarrow{{{u}_{1}}}=(1;-\sqrt{2};1);\overrightarrow{{{u}_{2}}}=(1;\sqrt{2};m)\Rightarrow \cos \left( {{d}_{1}};{{d}_{2}} \right)=\left| \cos \left( \overrightarrow{{{u}_{1}}};\overrightarrow{{{u}_{2}}} \right) \right|=\frac{\left| 1-2+m \right|}{2.\sqrt{{{m}^{2}}+3}}=\frac{\left| m-1 \right|}{2.\sqrt{{{m}^{2}}+3}}$

Do $\left( \widehat{{{d}_{1}};{{d}_{2}}} \right)={{60}^{o}}\Rightarrow \cos {{60}^{o}}=\frac{\left| m-1 \right|}{2\sqrt{{{m}^{2}}+3}}\Leftrightarrow \frac{\left| m-1 \right|}{2.\sqrt{{{m}^{2}}+3}}=\frac{1}{2}.$

$\Leftrightarrow \left| m-1 \right|=\sqrt{{{m}^{2}}+3}\Leftrightarrow {{m}^{2}}-2m+1={{m}^{2}}+3\Leftrightarrow m=-1.$

Bài tập 10: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $\left( \alpha \right):x-y+2z+1=0$ và đường thẳng $\Delta :\frac{x}{1}=\frac{y}{2}=\frac{z-1}{-1}.$ Góc giữa đường thẳng $\Delta $ và mặt phẳng $(\alpha )$ bằng

A. ${{150}^{o}}.$ B. ${{60}^{o}}.$ C. ${{30}^{o}}.$ D.${{120}^{o}}.$

Ta có$\overrightarrow{{{n}_{\alpha }}}=(1;-1;2);\overrightarrow{{{u}_{\Delta }}}=(1;2;-1)\Rightarrow \sin \left( \widehat{(\alpha );\Delta } \right)=\left| \cos \left( \widehat{\overrightarrow{{{n}_{\alpha }}};\overrightarrow{\Delta }} \right) \right|=\frac{\left| 1-2-2 \right|}{\sqrt{6}.\sqrt{6}}=\frac{1}{2}\Rightarrow \left( \widehat{\left( \alpha \right);\Delta } \right)={{30}^{o}}.$

Bài tập 11: Cho đường thẳng $d:\left\{ \begin{align} & x=6+5t \\ & y=2+t \\ & z=1 \\ \end{align} \right.$ và mặt phẳng $(P):3x-2y+1=0.$ Góc hợp giữa đường thẳng d và mặt phẳng (P) là:

A. ${{30}^{o}}.$ B. ${{45}^{o}}.$ C. ${{60}^{o}}.$ D. ${{90}^{o}}.$

Ta có $\overrightarrow{{{n}_{(P)}}}=(3;-2;0);\overrightarrow{{{u}_{d}}}=(5;1;0)\Rightarrow sin\left( \widehat{(P);\Delta } \right)=\left| \cos \left( \widehat{\overrightarrow{{{n}_{(P)}}};\overrightarrow{\Delta }} \right) \right|=\frac{\left| 15-2 \right|}{\sqrt{13}.\sqrt{26}}=\frac{1}{\sqrt{2}}\Rightarrow \left( \widehat{(P);\Delta } \right)={{45}^{o}}.$

Bài tập 12: Cho đường thẳng $d:\frac{x-3}{2}=\frac{y-2}{1}=\frac{z}{1}$ và mặt phẳng $(P):3x+4y+5z+8=0.$ Góc hợp giữa đường thẳng d và mặt phẳng (P) là:

A. ${{30}^{o}}.$ B. ${{45}^{o}}.$ C. ${{60}^{o}}.$ D. ${{90}^{o}}.$

Ta có $\overrightarrow{{{n}_{(P)}}}=(3;4;5);\overrightarrow{{{u}_{d}}}=(2;1;1)\Rightarrow \sin \left( \widehat{(P);\Delta } \right)=\left| \cos \left( \widehat{\overrightarrow{{{n}_{(P)}}};\overrightarrow{\Delta }} \right) \right|=\frac{\left| 6+4+5 \right|}{\sqrt{6}.\sqrt{50}}=\frac{\sqrt{3}}{2}\Rightarrow \left( \widehat{(P);\Delta } \right)={{60}^{o}}.$

Bài tập 13: Cho đường thẳng $d:\frac{x+1}{2}=\frac{y}{-1}=\frac{z-3}{1}$ và mặt phẳng $(P):3x-2y+5z+3=0.$ Gọi $\alpha $ là góc giữa đường thẳng d và mặt phẳng (P) khi đó $\sin \alpha $ bằng

A. $\frac{13}{2\sqrt{57}}.$ B. $\frac{13}{\sqrt{57}}.$ C. $\frac{13}{\sqrt{75}}.$ D. $\frac{13}{2\sqrt{75}}.$

Ta có $\overrightarrow{{{n}_{(P)}}}=(3;-2;5);\overrightarrow{{{u}_{d}}}=(2;-1;1)\Rightarrow \sin \left( \widehat{(P);\Delta } \right)=\left| \cos \left( \widehat{\overrightarrow{{{n}_{(P)}}};\overrightarrow{\Delta }} \right) \right|=\frac{\left| 6+2+5 \right|}{\sqrt{38}.\sqrt{6}}=\frac{13}{2\sqrt{57}}.$

Bài tập 14: Trong không gian tọa độ Oxyz cho đường thẳng $d:\frac{x}{1}=\frac{y-1}{-1}=\frac{z+2}{-2}$ và mặt phẳng $(P):2x+y-z+5=0.$ Góc giữa $d$ và (P) là:

A. ${{60}^{o}}.$ B. ${{45}^{o}}.$ C. ${{30}^{o}}.$ D. ${{150}^{o}}.$

Ta có $\overrightarrow{{{n}_{(P)}}}=(2;1;-1);\overrightarrow{{{u}_{d}}}=(1;-1;-2)\Rightarrow \sin \left( \widehat{(P);\Delta } \right)=\left| \cos \left( \widehat{\overrightarrow{{{n}_{(P)}}};\overrightarrow{\Delta }} \right) \right|=\frac{\left| 2-1+2 \right|}{\sqrt{6}.\sqrt{6}}=\frac{1}{2}.$

Suy ra $\left( \widehat{(P);\Delta } \right)={{30}^{o}}.$

Bài tập 15: Cho đường thẳng $d:\frac{x-1}{3}=\frac{y-1}{4}=\frac{z}{5}$ và mặt phẳng $(P):2x+my+mz-1=0.$ Gọi $\alpha $ là góc giữa đường thẳng d và mặt phẳng (P). Gọi S là tập hợp các giá trị của m sao cho $\alpha ={{60}^{o}}.$ Tổng các phần tử của tập hợp S là:

A. 0. B. – 19. C. – 18. D. – 20.

Ta có $\overrightarrow{{{n}_{(P)}}}=(2;m;m);\overrightarrow{{{u}_{d}}}=(3;4;5)\Rightarrow \sin \left( \widehat{(P);\Delta } \right)=\left| \cos \left( \widehat{\overrightarrow{{{n}_{(P)}}};\overrightarrow{\Delta }} \right) \right|=\frac{\left| 6+4m+5m \right|}{\sqrt{4+2{{m}^{2}}}.\sqrt{50}}$

$\Leftrightarrow \sin {{60}^{o}}=\frac{\left| 9m+6 \right|}{10\sqrt{{{m}^{2}}+2}}\Leftrightarrow \frac{\sqrt{3}}{2}=\frac{\left| 9m+6 \right|}{10\sqrt{{{m}^{2}}+2}}\Leftrightarrow 3.25\left( {{m}^{2}}+2 \right)=9{{(3m+2)}^{2}}$

$\Leftrightarrow 3(9{{m}^{2}}+12m+4)=25{{m}^{2}}+50\Leftrightarrow 2{{m}^{2}}+36m-38=0\Leftrightarrow \left[ \begin{align} & m=1 \\ & m=-19. \\ \end{align} \right.$

Cách dạng bài tập tính góc trong không gian oxyz: 2 mặt phẳng, 2 đường thẳng, dt và mp

Gọi $\varphi $ là góc giữa 2 mặt phẳng (P) và (Q) ta có:

$\cos \varphi =\left| \cos \left( \overrightarrow{{{n}_{(P)}}};\overrightarrow{{{n}_{Q}}} \right) \right|=\frac{\left| A.A'+B.B'+C.C' \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}+{{C}^{2}}}.\sqrt{A{{'}^{2}}+B{{'}^{2}}+C{{'}^{2}}}}({{0}^{o}}\le \varphi ,9{{0}^{o}})$

Cho 2 đường thẳng ${{d}_{1}}$ có vecto chỉ phương $\overrightarrow{{{u}_{1}}}=({{a}_{1}};{{b}_{1}};{{c}_{2}})$và đường thẳng ${{d}_{2}}$ có vecto chỉ phương $\overrightarrow{{{u}_{2}}}=({{a}_{2}};{{b}_{2}};{{c}_{2}})$. Góc $\varphi $ giữa hai đường thẳng đó được tính theo công thức

$\cos \varphi =\left| \cos \left( \overrightarrow{{{u}_{1}}};\overrightarrow{{{u}_{2}}} \right) \right|=\frac{\left| {{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}} \right|}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}.\sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}({{0}^{o}}\le \varphi ,9{{0}^{o}})$

Tích Vô Hướng, Tích Có Hướng Của Hai Vectơ trong không gian Oxyz và Ứng Dụng

Trong không gian với hệ tọa độ vuông góc Oxyz, tích vô hướng của hai vectơ (được định nghĩa giống như trong mặt phẳng), tích có hướng của hai vectơ (khái niệm không có trong mặt phẳng) được định nghĩa như sau (xem các ảnh dưới đây).

CÁC CÔNG THỨC DIỆN TÍCH, THỂ TÍCH CÓ LIÊN QUAN ĐẾN TÍCH VÔ HƯỚNG, TÍCH CÓ HƯỚNG

Nắm được các công thức này sẽ giúp học sinh lớp 12 học tốt chương phương pháp tọa độ trong không gian ở chương trình Hình học 12.

Cho hai vectơ \(\overrightarrow a  = ({a_1};{a_2};{a_3})\), \(\overrightarrow b  = ({b_1};{b_2};{b_3})\).

a) Biểu diễn từng vectơ \(\overrightarrow a \) và \(\overrightarrow b \) theo ba vectơ \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \)

b) Tính các tích vô hướng \({\overrightarrow i ^2},{\overrightarrow j ^2},{\overrightarrow k ^2}\), \(\overrightarrow i .\overrightarrow j \), \(\overrightarrow j .\overrightarrow k \), \(\overrightarrow k .\overrightarrow i \)

c) Tính tích vô hướng \(\overrightarrow a .\overrightarrow b \) theo toạ độ của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \).

Ba vectơ a→ ; b→ và c→ đồng phẳng nếu thỏa mãn một trong hai điều kiện sau:

- Giá của 3 vector đều cùng song song với mặt phẳng (P).

- 1 trong 3 vec tơ biểu diễn được qua hai vec tơ còn lại,

tức là tồn tại cặp số (m; n) duy nhất thỏa mãn

) Góc giữa đường thẳng và mặt phẳng

Cho đường thẳng d có vecto chỉ phương là $\overrightarrow{u}=(a;b;c)$ và mặt phẳng (P) có vecto pháp tuyến là $\overrightarrow{n}(A;B;C)$. Gọi $\varphi $ là góc giữa d và (P) thì $\varphi $ được tính theo công thức

$\sin \varphi =\left| \cos \left( \overrightarrow{u};\overrightarrow{n} \right) \right|=\frac{\left| A.a+B.b+C.c \right|}{\sqrt{{{A}^{2}}+{{B}^{2}}+{{C}^{2}}}.\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}({{0}^{o}}\le \varphi ,9{{0}^{o}})$